Vasudev Sharma

Vasudev Sharma

MSc in Applied Computing

SimCLR Visually Explained

5 minute read

Published:

This blog post serves as a primer for SimCLR, a framework for self-supervised visual representation learning using contrastive learning.

Fig.: Architecture of SimCLR

What is SSL (Self-Supervised-learning)?

Importance of SSL in Vision

ImageNet has approx 14 million natural images, categorized by 20K objects and it took approx 22 human years to label it. Labeling a dataset is expensive task, necessary for the success of supervised algorithms. However, it is infeasible to manually annotate images. This is a fundamental problem is application areas such as Medical Imaging, where not only it is extremely expensive operation but also it requires expertise of subject-matter.

SSL is an unsupervised learning algorithm which leverages the unlabelled data to generate supervision signal which after being pre-trained can be used for downstream tasks, such as classification, recognition, segmentation, etc without the impediment of labels, necessary for supervised learning.

Contrastive Learning ☯

Similar images should have similar embeddings.

Using this idea, several contrastive learning frameworks (SimCLR, PIRL, MoCo, SWaV) have been developed lately

For this blog post, we will understand SimCLR.

SimCLR Key Idea 💡

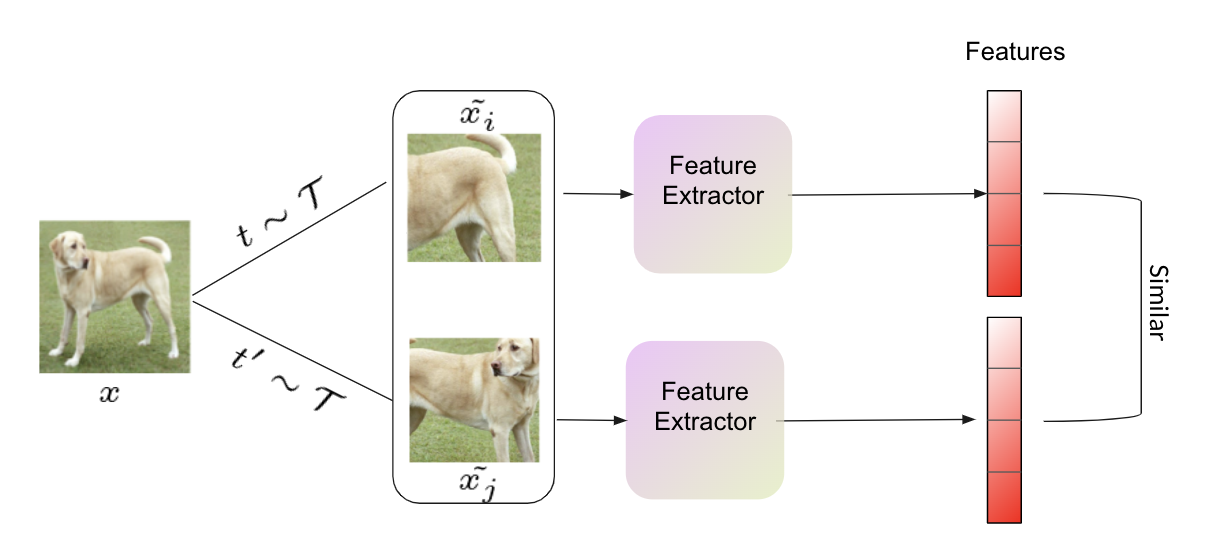
Idea: An image when distorted by data augmentations would produce same features.

For instance, let say we sample two augmentations $t$ and $t’$ sampled from a family of transformations $\mathcal{T}$. Given an input image x, under the data augmentations it should be data augmentation invariant. That is,

\[\text{features(t(x))} = \text{features(t'(x))}\]

SimCLR Architecture Visually explained

Following the key idea, that is, the features should be data-augmentation invariant, the feature embeddings below is the architecture of SimCLR.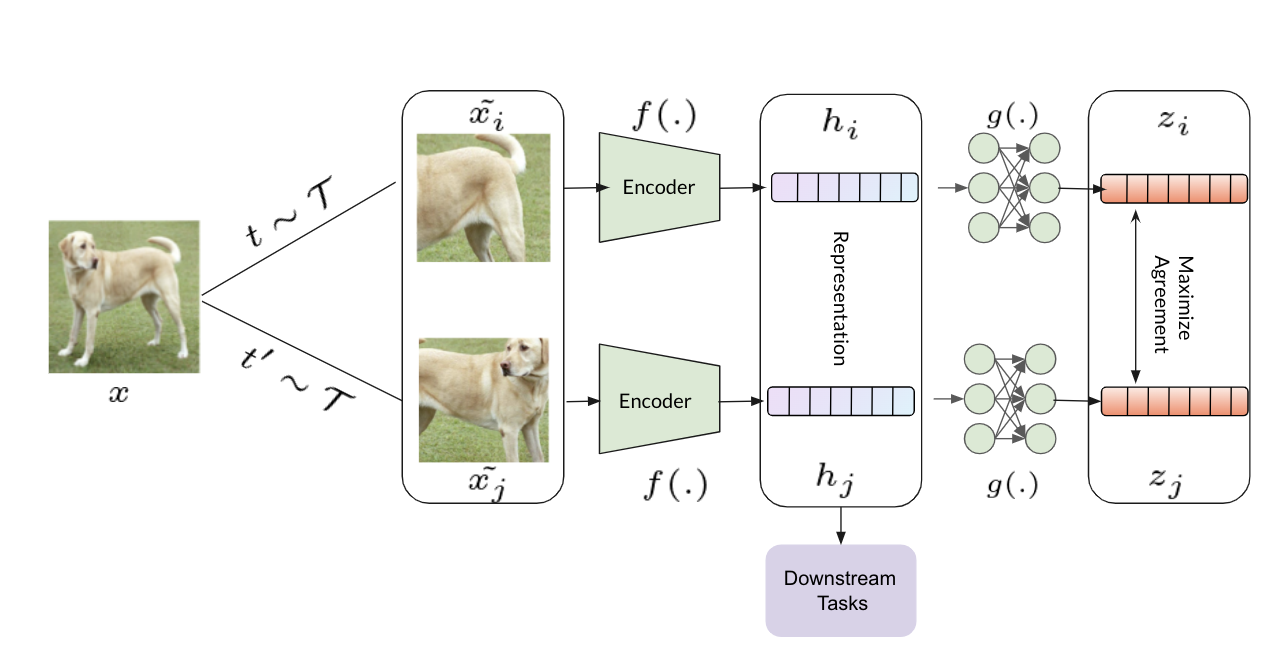

Lets distill the architecture step by step:

  • Data Augmentation The first and foremost step is to distort an image to generate 2 noisy views sampled from a family of data augmentations $\mathcal{T}$. In SimCLR paper, color distortion (jittering + color dropping), Gaussian Blur, and Cropping ($224 \times 224$) as a composition of data augmentation are used, yielding the best performance on ImageNet top-1 accuracy.

    Out of all the data augmentations authors tried, Color distorting and Crop-out stood out. Unlike supervised data augmentations, one needs to carefully select the best data augmentation for the pre-training tasks as evidenced by the ablation studies in the paper.

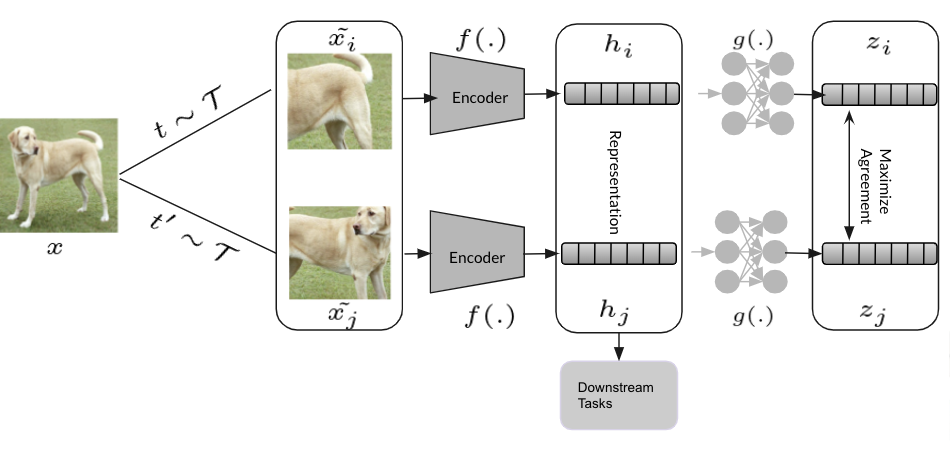
  • Hidden Representation Afterwards, a network $f(.)$ (typically a neural network) encodes the views into hidden representations $h_i$ and $h_j$ respectively.

    Once the whole network is pre-trained using the SimCLR framework, network $g(.)$ can be thrown away and the learned hidden representations $h$ can be used for a variety of downstream tasks.

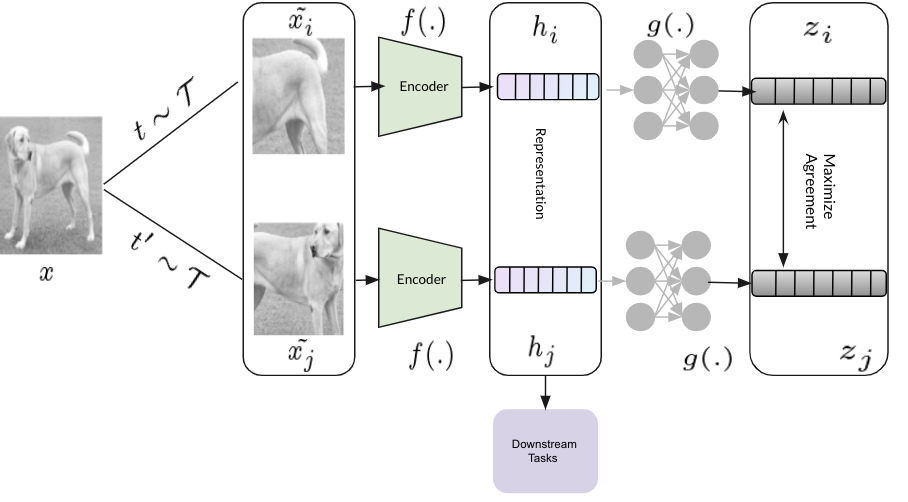
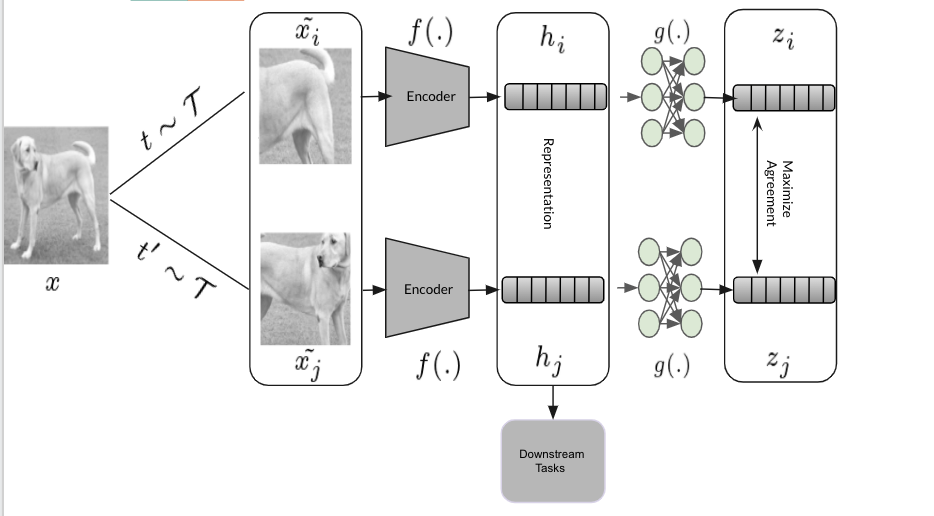
  • Projected Embeddings A projection network $g(.)$, projects the hidden representations into latent space $z$. Here, $g(.)$ is a 2 layer non-linear(ReLU) multi layer perceptron.

    The key takeaway is that it uses a non-linear projection head as apposed to linear or no projection head as more information is lost upon doing so and it has been demonstrated empirically by the authors. For more details, refer to the paper.

  • Maximize agreement The last step is to maximize the learned projected embedding/representation (objective function) using contrastive loss, a variant of Cross-Entropy loss, NT-Xnet loss(Normalized Temperature scaled Cross Entropy loss)

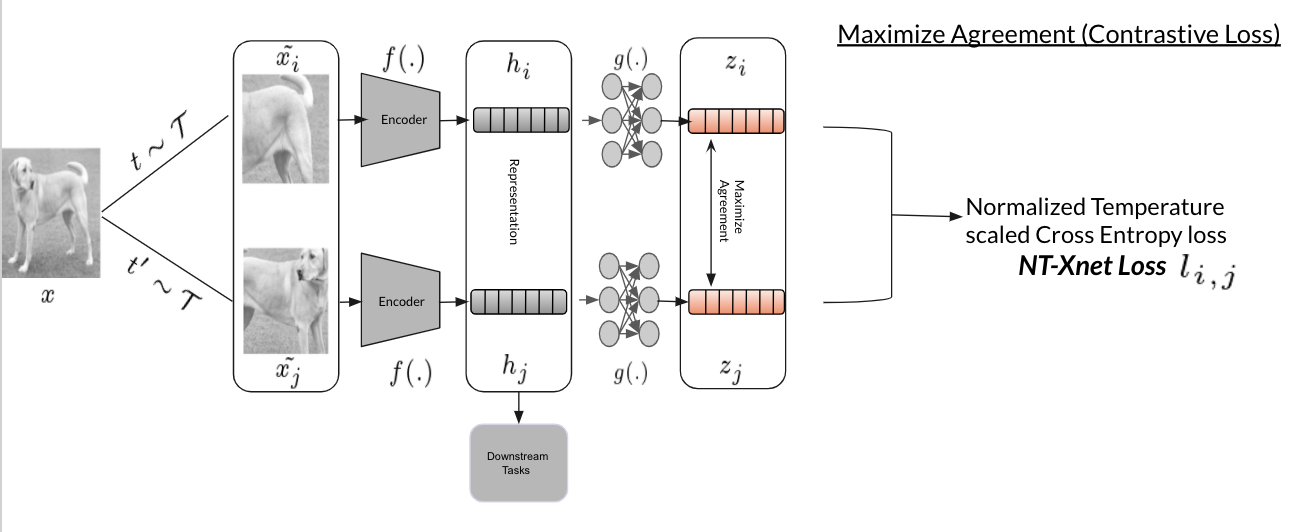
    Since $z_i$ and $z_j$ are the same views of the anchor image $x$, it is considered as a positive pair of an image $x$. Other views in a given batch relative to $z_i$ and $z_j$ are negative samples and considered as negative pairs.

    Contrastive Loss

    The similarity between two representations $u$ and $v$ can be computed using the cosine similarity as mentioned below:
    \begin{aligned} \text{sim}(u,v)=u^{\top}v/||u||\ ||v|| \end{aligned}

    Since it uses cosine similarity for computing the similarity between the representations rather than dot product ($u^Tv$), it normalizes ($l_2$ normalization) the representations.

    The contrastive loss is formally represented by $l_{i, j}$ as:

    \begin{aligned} l_{i, j} = -log \frac{exp(sim(z_i, z_j)/\mathcal{T})}{\sum_{k=1}^{2N}1_{[k\neq i]}exp(sim(z_i, z_j)/\mathcal{T})} \end{aligned}

    The numerator quantifies the similarity between the positive pair, while the denominator quantifies the similarity between the anchor representation $z_i$ and negative samples $\forall k \neq i$, constituting a negative pair.

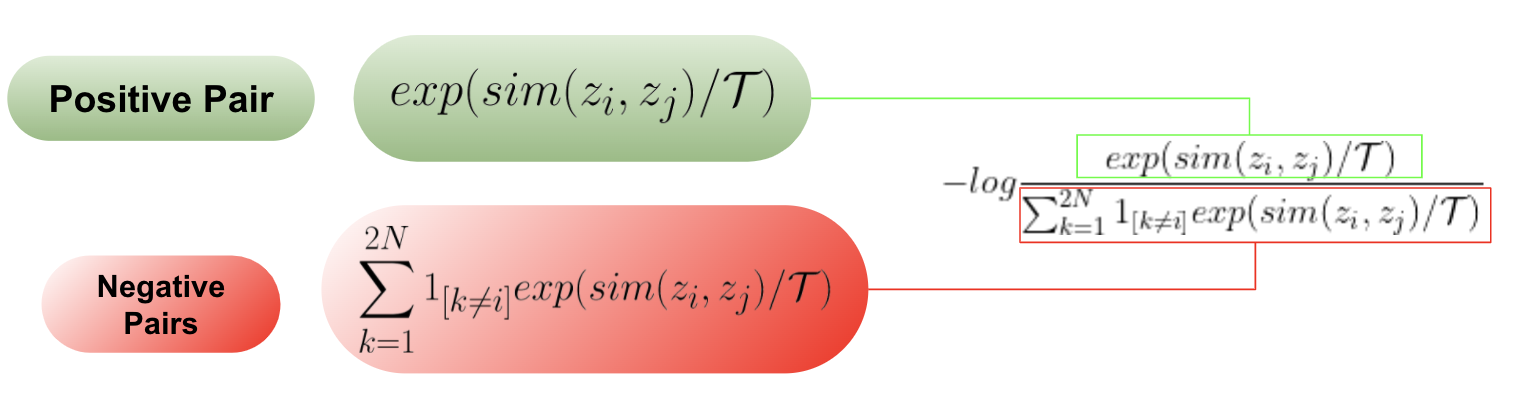
SimCLR Animation

Given a set of images in a batch, during the training objective, the negative pairs (different views)“repel” (dissimilar) each other, while the (similar views) “attract” each other. This is achieved via contrastive loss.

SimCLR Advantages

  • Simplistic yet powerful framework for unsupervised visual representation learning.
  • Pre-trained representations can be straightaway used for a number of downstream tasks compared to pre-text based self-supervised learning.

SimCLR Disadvantages

  • For successful pre-training of any contrastive learning method, large negative samples are necessary. Hence, a large batch size (typically more than 8K) is required for SimCLR to learn effectively.

Citation

@misc{vasudev2021simclr,
  title   = {SimCLR visually explained},
  author  = {Vasudev Sharma},
  year    = 2022,
  note    = {\url{https://vasudev-sharma.github.io/posts/2022/03/SimCLR-visually-explained/}}
}

References

You May Also Enjoy